Stratégie de contrôle de la hauteur dans les instruments de musique numériques
Vincent Goudard, Lionel Feugère et Hugues Genevois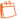 novembre 2016
novembre 2016Résumés
Résumé
Dans de nombreuses cultures, la musique se construit sur des échelles de hauteurs qui jouent un rôle prédominant dans la lutherie. Mais la liberté de mapping1 que permettent les ordinateurs, ainsi que la diversité des interfaces, donne lieu à une grande variété de stratégies pour le contrôle de la hauteur dans les instruments numériques. Sans prétendre être exhaustif, cet article tente de donner une vue d’ensemble, en proposant : 1) une revue des interfaces pour produire des hauteurs discrètes et/ou continues ; 2) une revue des stratégies de lutherie numérique proposant à l’instrumentiste un contrôle facilité et précis de la hauteur ; 3) des algorithmes développés par les auteurs concernant le contrôle continu de la hauteur ; 4) quelques comparaisons avec les instruments acoustiques. Enfin, un patch Max est disponible publiquement pour étayer cet article et permettre au lecteur de tester des stratégies de mapping présentées dans cet article.
Notes de l'auteur
Cet article dresse un panorama des techniques de contrôle de la hauteur monodique dans les instruments de musique numérique (DMI - Digital Music Instrument), en particulier de son contrôle manuel et précis.
1. Introduction
1L’opposition entre le continu et le discret est une question qui, au-delà de l’univers musical, traverse l’histoire de la philosophie et des sciences depuis l’antiquité, et qui recouvre parfois une autre opposition, celle qu’il est courant d’établir entre le catégoriel et le quantitatif. Dans le domaine musical, la quantification des hauteurs et des durées sur des échelles ou des grilles est omniprésente. L’écriture musicale occidentale témoigne de cette catégorisation.
2Pourtant, de nombreux instruments ainsi que la voix chantée permettent de glisser d’une note à l’autre de manière continue. Le xxe siècle a aussi vu naître de nouvelles lutheries offrant à l’interprète la possibilité de jouer des glissandi comme le Theremin ou l’Onde Martenot (Loriod, 1987). Par ailleurs, certains compositeurs, Iannis Xenakis (Xenakis, 1963) en particulier, ont imaginé des univers sonores non quantifiés, écrivant des pièces qui explorent le continuum sonore. Metastasis, créée en 1955 au Festival de Donaueschingen, est une des œuvres les plus emblématiques de ces recherches.
3Si la notion de hauteur, et les théories de l’harmonie qui l’accompagnent, est un très vaste champ d’étude, cet article se focalise sur les techniques permettant de contrôler précisément la hauteur monodique sur un instrument de musique numérique. Nous présentons des interfaces et algorithmes offrant la possibilité d’un contrôle discret ou continu des hauteurs et en proposons une implémentation2 articulée dans le logiciel Max3et disponible sur le site du LAM4
2. Perception et production de la hauteur
2.1 Perception de la hauteur
4Le système auditif permet de distinguer de très petites variations de hauteur. Dans le cas de voyelles synthétiques de fréquence fondamentale comprise entre 80 et 120 Hz, la plus petite variation perceptible varie entre 5 et 9 cents (Flanagan, Saslow, 1958).
5Le sens commun tend à associer la hauteur perçue à la fréquence fondamentale d’un son harmonique, mais la psychoacoustique a montré combien cette perception peut être contextuelle et culturelle (Castellengo, 1994).
6Certains instruments permettent la sélection d’harmoniques qui prennent chacun leur autonomie comme si deux mélodies se superposaient (didgeridoo, guimbarde, chant diphonique). D’autres présentent des vibrations non linéaires, comme les cloches, dont le timbre non harmonique rend malaisé la distinction d’une hauteur prédominante. Certains tambours ne fournissent quant à eux pas de fréquence fondamentale précisément perceptible, car leur son est constitué d’une large bosse spectrale ou d’une fréquence fondamentale évoluant rapidement avec le temps.
7La perception de hauteur s’appuie donc sur deux mécanismes différents : un « codage temporel » (mesuré en tonie) et une hauteur spectrale (« tonotopie », mesuré en chromie)5. Ces deux modes de perception, s’ils existent de manière distincte, se superposent et la frontière supposée les séparer est floue. Les sons de Shepard (Shepard, 1964) et Risset mettent en évidence cette intrication6.
2.2 La production de hauteur dans les instruments acoustiques
8L’émergence d’une hauteur est le plus souvent liée à un phénomène de résonance, qui filtre toutes les fréquences autres que les harmoniques d’une fréquence fondamentale (ce qui n’est pas nécessairement le cas dans le domaine numérique, comme nous le verrons ci-après). Différentes hauteurs peuvent ainsi être obtenues :
-
en jouant sur une multitude d’éléments accordés différemment (les cordes d’une harpe, les lames d’un marimba, etc.) ;
-
en modifiant les caractéristiques d’un élément résonnant, le plus souvent sa longueur (tube des instruments à vent, corde d’un violoncelle) ;
-
en sélectionnant des harmoniques précis d’un son riche (didgeridoo, chant diphonique).
9Ces techniques peuvent être employées conjointement, par exemple lors de la modulation d’une hauteur autour d’une valeur de référence : l’instrumentiste peut ainsi moduler la tension d’une corde pour altérer la hauteur, ou choisir une autre corde pour changer la hauteur de manière plus franche.
2.3 Production de hauteur dans les instruments numériques
10Dans les instruments numériques, la production de la hauteur d’un point de vue mécanique n’intervient qu’au niveau du haut-parleur, quand celui-ci est excité par un signal électrique. La hauteur émanant de ce signal peut résulter d’un ou plusieurs processus liés :
-
à la vitesse de lecture d’une table d’onde (synthèse additive, sample/granulaire, FM, etc.) ;
-
au contenu de cette table d’onde ;
-
au délai de réinjection d’un filtre résonnant (synthèse soustractive, Karplus, etc.) ;
-
à un filtrage dans le domaine fréquentiel (FFT, etc.).
11Les hauteurs résultantes sont ainsi découplées du corps de l’instrument acoustique. La hauteur « symbolique » (comparable à celle notée dans une partition) devient une variable numérique manipulable par des algorithmes.
3. Les interfaces de jeu
12La plupart des instruments acoustiques donnent la possibilité au musicien de jouer sur une échelle discrète à l’aide de clés, de touches, de frettes pour mettre en vibration l’instrument à des fréquences précises réglées lors de la lutherie et de l’accordage. Quelques instruments offrent la possibilité de produire un glissando continu comme le violoncelle, le trombone, ainsi que, dans une moindre mesure, des instruments à vent comme la flûte bansuri, par des modes de jeu appropriés. Des accessoires permettent également, dans certains cas, de s’affranchir de la discrétisation propre à l’instrument (e.g bottleneck de guitare). Enfin, quelques automates mécaniques comme les boîtes à musique ou les orgues de barbarie permettent un jeu de hauteur, généralement discret, faisant usage d’un matériel précomposé. Nous allons voir comment ces interfaces sont transposées dans le monde numérique.
3.1 Spécificités des instruments numériques
13Les instruments de musique numériques sont très récents dans l’histoire de la musique, et intègrent des spécificités propres à leur nature (Cance, Genevois, Dubois, 2013). Certaines de ces caractéristiques se retrouvent dans les instruments électriques, comme le découplage énergétique entre le geste de l’instrumentiste et le son produit, et le découplage spatio-temporel qui en résulte.
14D’autres caractéristiques sont propres aux instruments numériques, comme l’intégration du symbolique dans l’instrument et la grande rapidité de calcul symbolique que proposent les ordinateurs, la plus grande souplesse dans les mémoires et les réglages de l’instrument, la nature évolutive des logiciels et la modularité des interfaces physiques (hardware) et des algorithmes de synthèse audio qui en découle (Cadoz, 1999).
15Le choix des capteurs utilisés pour contrôler les variables des algorithmes décrits dans les sections suivantes est une question aussi cruciale que complexe, que nous ne traiterons pas dans cet article. Nous renvoyons les lecteurs intéressés vers les articles suivants qui traitent de ces questions : (Vertegaal, Ungvary, Kieslinger, 1996), (Wanderley, Viollet, Isart, Rodet, 2000), (Marshall, Hartshorn, Wanderley, Levitin, 2009).
3.2 Interfaces pour hauteurs discrètes
3.2.1 Claviers
16La notion d’échelle a une forte influence sur la disposition des hauteurs sur le corps de l’instrument. Ainsi, le clavier de piano est une interface permettant de jouer toutes les hauteurs de la gamme chromatique, disposées selon la gamme de Do majeur. Sa grande notoriété a poussé à utiliser cette organisation pour les claviers des premiers synthétiseurs.
17Cependant, les claviers dits « isomorphiques », inspirés du Tonnetz de Euler, proposent une autre ergonomie. La table harmonique ou le système Wicki-Hayden (figure 1) proposent ainsi une organisation des hauteurs qui permet de conserver le même motif intervallique indépendamment de la transposition. On observe aujourd’hui un intérêt croissant pour ce genre de clavier (Flanagan, Saslow, 1958) et plusieurs fabricants indépendants ou industriels l’ont adopté pour leurs interfaces7.
Figure 1. Agencements des notes en (a) et table harmonique (b
Les deux se trouvent implémentés et intégrés à la librairie du LAM.
Source : selon Wicki-Hayden
18D’autres exemples de mapping ont été recensés par les auteurs, parmi les multiples réalisations de prototypes d’instruments — du piano préparé aux instruments numériques — notamment : une tonalité dynamique (Milne, Sethares, Plamondon, 2007), des courbes chaotiques pour jouer délibérément des mélodies ou accords instables tout en gardant un geste consistant sur la surface de jeu (Dabby, 1996) ; des échelles avec des notes répétées pour obtenir une sorte de bourdon, des intervalles hétérogènes multiples ou encore des interpolations d’octaves.
3.2.2 Claviers incrémentiels/séquenceurs
19Quelques instruments ont été développés permettant de jouer un intervalle plutôt qu’une hauteur, le Samchillian8 est vraisemblablement le plus connu. Malgré l’intérêt que suscite ce type de clavier pour les productions de mélodies et d’arpèges, cet instrument ne fait pas encore l’objet d’une production à échelle industrielle ni d’un usage répandu.
20Le séquenceur contient une partition généralement constituée de notes définies par leur hauteur, leur intensité et leur durée. Une manière « instrumentale » de jouer d’un séquenceur a été étudiée par Jean Haury avec son « méta-piano » (Haury, 2008). Son idée est de laisser au séquenceur le contrôle de la suite de hauteur et la vélocité relative, et de conserver, pour l’interprétation, la vitesse d’exécution, l’agogie, le phrasé et l’intensité9.
21Il est aussi possible de recourir à des modèles de comportement dynamiques (De Laubier, Teruggi, 1991) qui joueront les hauteurs en suivant une évolution propre à leur comportement. Dans ce cas, les hauteurs peuvent être choisies au préalable comme un set de valeurs qui seront jouées en étant mixées, interpolées, ou déclenchées selon le modèle intermédiaire. Les deux premiers auteurs de cet article ont présenté de tels modèles dans l’article “Dynamic intermediate models for audiographic synthesis” (Goudard, Genevois, Doval, Ghomi, 2011).
3.3 Interfaces pour le continuum fréquentiel
22La volonté de s’affranchir de quantifications fréquentielles trop rigides se manifeste aujourd’hui dans de nombreuses inventions qui témoignent d’un même désir de liberté et d’expressivité. Nous citerons à titre d’exemple le Continuum Fingerboard10, le LinnStrument11, le Seaboard12 et enfin le Theremini 13. Chacun de ces instruments tente, à sa façon, de réconcilier le continu et le discret en permettant de passer le plus souplement possible de l’un à l’autre.
23Bien que détournée de son usage initial, une interface souvent utilisée pour jouer les hauteurs est la tablette graphique (Zbyszynski, Wright, Momeni, Cullen, 2007). En offrant une grande précision de mesure14, cette surface a donné lieu à différents prototypes d’instruments et a été évaluée comme une interface valable pour le contrôle de l’intonation de la parole, au moins aussi précise que la voix naturelle lors d’une expérience d’imitation prosodique (d’Alessandro, Rilliard, Le Beux, 2011). Une récente expérience du LIMSI a montré que de nombreuses personnes étaient capables de jouer de manière plus juste avec la tablette qu’avec leur propre voix (d’Alessandro, Feugère, Le Beux, Perrotin, Rilliard, 2014).
4. Les techniques de jeu
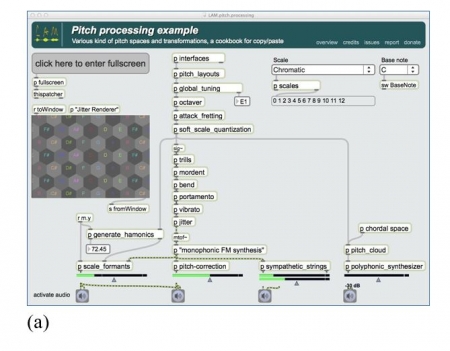
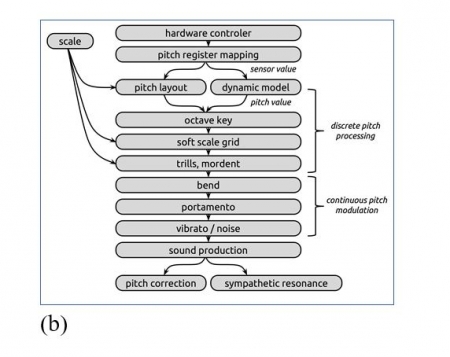
24Le jeu sur la hauteur peut ainsi s’envisager selon trois axes complémentaires : un jeu sur le continuum fréquentiel, un jeu sur échelle avec les ornements traditionnels tels que trilles et appoggiatures, et un jeu de modulations à l’intérieur de l’échelle telles que le vibrato ou le bend. Nous avons essayé d’organiser logiquement ces parties afin de pouvoir les utiliser de manière complémentaire. La figure 2 illustre cette organisation, qu’on retrouve dans le programme Max associé à cet article.
Figure 2. Vue d’ensemble (a) des modules de traitements de la hauteur et (b) du patch Max associé
4.1 Traitement pré-échelle : mapping continu
25Dans le cas d’instruments numériques, l’interface physique renvoie des valeurs de capteurs qui peuvent ne pas être directement corrélées avec les axes souhaités pour le jeu musical. Un premier niveau de mapping consiste à convertir les données issues des capteurs vers un système de coordonnées ergonomique pour le contrôle de la hauteur.
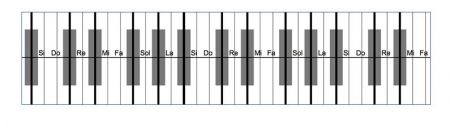
26L’instrument mis au point pour le Cantor Digitalis (Feugère, d’Alessandro, 2015) propose un mapping linéaire de la hauteur sur l’axe gauche-droite de la tablette représenté par un clavier de piano anamorphosé collé sur la tablette (figure 3). Son intérêt réside dans la transformation du clavier traditionnel — des hauteurs discrètes sur des touches espacées de manière non linéaire — en un clavier continu et linéaire, tout en conservant les repères visuels d’une représentation en touches blanches et noires du piano.
Figure 3. Le clavier du Cantor Digitalis du LIMSI
27Les lignes verticales correspondent aux hauteurs chromatiques. Les lignes en gras correspondent aux frontières des touches traditionnelles. Les lignes en gras entre Si et Do et entre Mi et Fa sont manquantes pour conserver la linéarité de la hauteur.
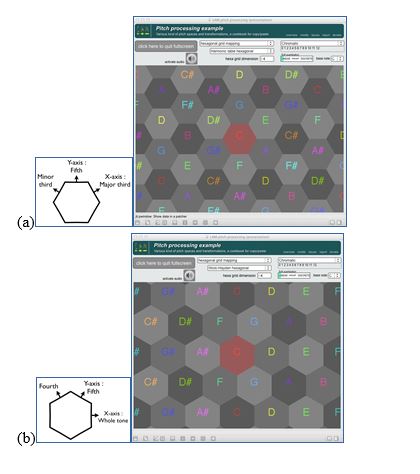
28Le Voicer (Kessous, 2002) permet un contrôle de la hauteur le long d’une spirale sur la tablette ; un tour étant associé à l’octave (figure 4). Le HandSketch (D’Alessandro, Dutoit, 2007) propose une courbure correspondant à la rotation naturelle du bras selon l’articulation du coude, une idée similaire se retrouvant dans des claviers de pianos acoustiques expérimentaux (Haury, 1999) (figure 5).
Figure 4. Le mapping en spirale de la hauteur illustré dans la librairie du LAM, comme dans le Voicer
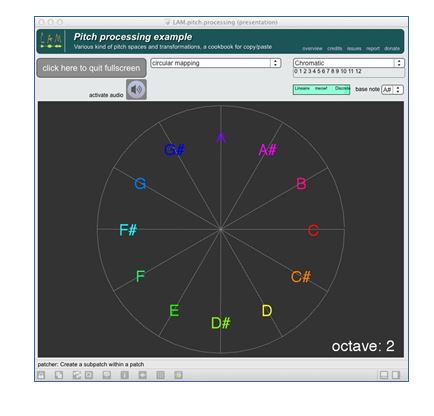
Dans le patch du LAM, l’octave est automatiquement décalée à chaque fois que la note de référence est franchie, afin de préserver le continuum de la hauteur.
Source : auteur
Figure 5. (a) Deux claviers ergonomiques : celui du dessus présente différentes orientations des touches, tandis que celui du dessous a une forme courbe. (b) Le mapping en courbe de la hauteur, implémenté et intégré à la librairie du LAM
Source : auteur d’après Haury, 1999
4.2 Clé d’octave, changement de registre et transposition
29En raison de l’organisation prépondérante des hauteurs selon l’octave, la clé d’octave conserve un intérêt dans les instruments numériques en ce qu’elle permet d’accéder à d’autres registres — plus graves ou plus aigus — tout en conservant l’équivalence spatiale des notes sur la topologie de l’instrument. De plus, elle permet d’étendre le registre potentiel d’un instrument, en conservant une surface de jeu compacte. Outre le cas particulier de l’octave, la transposition de tout l’espace de jeu permet à l’instrumentiste de s’adapter à différents diapasons, de jouer des partitions écrites pour des instruments transpositeurs (par ex. la clarinette), ou de changer l’accordage de l’instrument pour des raisons stylistiques.
30Il est également possible d’utiliser le principe de circularité de hauteur (Charbonneau, Risset, 1973) afin de passer de manière continue d’une octave à l’autre15.
4.3 Mapping à l’échelle
4.3.1 Banque d’échelles
31Une organisation essentielle de la hauteur est l’échelle, qui sélectionne un certain nombre de degrés dans le continuum fréquentiel. Un grand nombre d’échelles tonales et microtonales ont été implémentées dans une banque d’échelles directement accessibles sous forme de liste. Leurs valeurs sont exprimées en valeur flottante de demi-tons, relativement à une note de référence arbitraire, de manière similaire au format scala16. Le dernier intervalle représente l’intervalle de repliement. Par exemple, pour la plupart des échelles basées sur l’équivalence d’octave, le dernier intervalle sera 12. Les échelles non octaviantes, comme le système de Bohlen-Pierce (se repliant sur le tritave) ou les échelles qui ne se replient pas du tout, sont également possibles dans ce système.
4.3.2 Échelles adaptatives
4.3.2.1 Frettage réglable
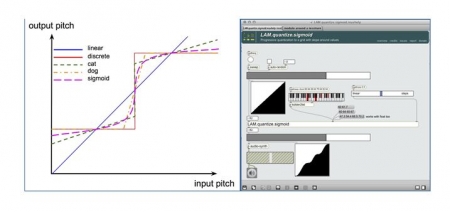
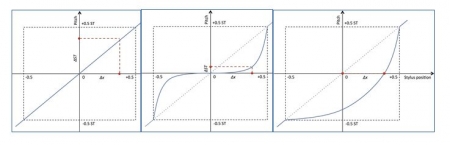
32Dans le cadre du programme Orjo (2009-2012), soutenu par l’Agence nationale de la recherche, le LAM a développé des fonctions de mapping permettant de passer de manière continue d’une échelle discrète donnée à une échelle continue, en passant par un état semi-discret comme présenté dans l’ouvrage de Favilla (1996). Une variable allant de 0 % (pitch continu) à 100 % (pitch discret), permet de doser la dureté du frettage. Il existe trois variantes de cette fonction : « cat », « dog » et « sigmoid » (figure 6). Les deux premières doivent leur nom à la transition douce (« meow ») ou raide (« woof ») entre notes de l’échelle. La troisième est un intermédiaire entre ces deux versions.
Figure 6. (a) Une vision schématique des transitions de la hauteur entre les algorithmes « cat », « dog » and « sigmoid », and (b) le patch Max associé
Source : auteur
33L’algorithme de LAM.quantize.cat en pseudo-code :
Soit 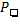 la valeur de pitch à quantiser
la valeur de pitch à quantiser
Soit 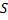 la liste des valeurs constituant l’échelle filtrante
la liste des valeurs constituant l’échelle filtrante
Soit 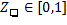 la dureté du frettage.
la dureté du frettage.
Pour 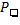 , on cherche
, on cherche 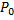 et
et 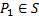 , les valeurs de l’échelle directement inférieures et supérieures respectivement à
, les valeurs de l’échelle directement inférieures et supérieures respectivement à 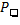
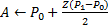
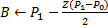
IF 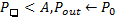
ELSE IF 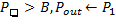
ELSE 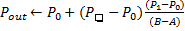
4.3.2.2 Frettage d’attaque
34Pouvoir attaquer une note juste sur une surface non frettée est une autre difficulté. On peut facilement, à l’oreille, « rattraper » la note juste, mais cette réponse tardive n’est pas toujours satisfaisante. Perrotin et d’Alessandro (Perrotin, d’Alessandro, 2013) ont développé un système adaptatif permettant d’obtenir une hauteur juste à l’attaque, en anamorphosant dynamiquement l’axe des hauteurs afin de préserver le continuum (voir figure 7).
Figure 7. Mapping entre la position d’un pointeur physique sur une surface 2D avec la hauteur en coordonnées relatifs
À droite : mapping pour une note juste à l’attaque et un minimum d’impact sur le continuum autour de la note visée
Source : d’après Perrotin & d’Alessandro [20]
Le LAM a développé une nouvelle version de cet algorithme pour répondre aux cas d’échelles non-chromatiques, et coller au degré le plus proche dans une échelle possiblement microtonale. Soit 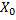 la valeur de hauteur au moment du touché et
la valeur de hauteur au moment du touché et 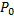 la hauteurs la plus proche,
la hauteurs la plus proche, 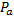 la hauteur directement plus basse et
la hauteur directement plus basse et 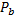 la hauteur directement plus haute dans une gamme donnée, le coefficient gamma de correction est donné par la formule :
la hauteur directement plus haute dans une gamme donnée, le coefficient gamma de correction est donné par la formule :
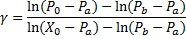
35et la hauteur corrigée Y peut être calculée à partir de l’entrée X avec la formule :
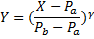
4.4 Modulation relative à l’échelle : mordant, trille, gruppetto, turn, arpèges, fall
36Tous ces ornements sont habituellement joués de manière relative à une échelle courante, potentiellement altérée. Un trille consiste en l’alternance rapide entre deux degrés proches. Un mordant est similaire mais limité à une seule alternance. De même, la vitesse d’alternance est liée au tempo.
37Difficile avec certains instruments acoustiques comme la voix naturelle, cela est rendu possible avec leurs analogues numériques. Par exemple, en utilisant un DMI pour modéliser le son de la voix, D’Alessandro & Tutoit (D’Alessandro, Dutoit, 2007) combinent le contrôle continu de la tablette graphique, pour les portamenti, avec des capteurs FSR17 ajoutés à la tablette afin de jouer des trilles en s’aidant de techniques de guitare.
38Le LAM a implémenté un trille automatique à la fréquence audio, prenant comme entrées le degré (positif ou négatif) d’alternance, l’échelle courante et la fréquence du trille. Le relâchement du trille est effectué en fournissant un degré nul ; pour sa part, l’algorithme s’assurera que le trille finisse correctement, sans couper la dernière note en cours.
4.5 Modulation post-échelle
4.5.1 Portamento
39Le portamento peut être facilité par l’interpolation spatiale et le frettage adaptatif décrit précédemment, mais il peut également être accompli par une interpolation temporelle.
Il est alors intéressant d’utiliser un filtre passe-bas résonant. Il en résulte deux paramètres pour contrôler l’effet : la fréquence F et la résonance Q du filtre. Pour une meilleure ergonomie, la résonance peut être exprimée en fonction du demi-temps de relâchement18 (T), par la formule : 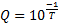 .
.
40Cet algorithme fournit à la fois une transition lisse s’il est réglé avec des valeurs telles que F = 2 Hz et T = 500 ms, ou vibration s’apparentant au vibrato avec des réglages tels F = 7 Hz et T = 5 000 ms. Pour des grandes valeurs de F, de riches attaques transitoires cuivrées sont produites.
4.5.2 Bend
41Le bend est un effet utilisé sur certains instruments à corde obtenu en tirant la corde pour transposer temporairement la note quelques demi-tons plus haut. Il est aussi possible d’abaisser la hauteur de la note en effectuant un release-bend sur une corde préalablement tirée.
42Une touche de guitare peut être « scallopée » en creusant entre les frettes pour former de petites cuvettes en « U ». Cela permet au guitariste de pincer la corde sans contact avec la touche et rend plus aisée la réalisation des bends, à la fois parce que cela élimine les frictions entre doigt et touche, mais permet aussi de modifier la hauteur en appuyant plus ou moins fort sur la corde. La touche « scallopée » existe traditionnellement dans certains instruments indiens tels que la vînâ (figure 8), facilitant les variations microtonales propres à la musique indienne.
43Dès les années 1930, différents systèmes sont utilisés sur les guitares électriques pour produire des variations de hauteurs à l’aide d’une whammy bar19 (figure 9), typiquement au chevalet. Ce levier permet de faire varier rapidement la tension et parfois la longueur de toutes les cordes simultanément pour créer un vibrato, portamento ou des effets de bend.
44Les molettes de pitch bend placées sur les claviers peuvent faire évoluer la note d’un facteur beaucoup plus important et dans les deux directions de hauteur. Une des particularités du bend est l’effort nécessaire à la production du changement de hauteur, contrairement au retour de la hauteur à sa valeur d’origine ne nécessitant pas ou peu d’effort. Notre implémentation du bend prend en compte cette particularité.
Figure 8. Une vînâ Saraswati avec ses frettes scaloppées
Figure 9. Une Gibson Les Paul équipée d’une barre de vibrato Bigsby
4.5.3 Vibrato
45Le vibrato est une modulation de la hauteur mélodique autour d’une valeur centrale. Il peut être caractérisé par deux facteurs : l’ampleur et la fréquence de la modulation. Dans le cas d’un chanteur soprano, la fréquence de modulation varie typiquement entre 4 et 8 Hz et l’ampleur s’étend de 20 à 150 cents (Ferrante, 2011).
46Une simple implémentation consiste à moduler la hauteur avec un LFO20. Compte tenu de la fréquence de variation du vibrato, cette modulation doit être échantillonnée à une fréquence d’au moins 20 Hz. En plus de la fréquence et de l’ampleur du vibrato, nous avons ajouté un paramètre de finesse agissant sur le degré de saturation de l’onde sinusoïdale modulante et rendant le vibrato plus abrupt lorsque le gain augmente.
4.6 Effets secondaires de la modulation de la hauteur
47La vivacité du son des instruments acoustiques est en partie due au fait que la modulation de la hauteur n’agisse pas sur une seule caractéristique du son à la fois. Par exemple, (Shepard, 1964) on observe que des traits comme le centre spectral, l’intensité perçue, ou la répartition des harmoniques pairs et impairs sont également affectés par le geste de vibrato.
48Grâce au design modulaire de notre implémentation, il est possible de récupérer le signal modulé à chaque étage de traitement. En fonction du choix de l’algorithme de synthèse sonore, il est ainsi possible d’utiliser ces signaux pour agir sur le timbre et la dynamique.
5. Perspectives
49La recherche et les méthodes décrites dans cet article ne couvrent pas complètement le sujet, et l’implémentation que nous proposons simplifie grandement la complexité du contrôle des instruments numériques par rapport aux contraintes physiques des instruments acoustiques.
50Par ailleurs, nous n’adressons pas ici la question de la polyphonie, ce que nous projetons de réaliser dans le futur, ni celle de l’évolution interne de la hauteur dans les évènements sonores déclenchés21. Cependant, nous espérons que ce travail contribue à donner un aperçu de la façon dont la hauteur peut être jouée de manière monophonique, de la conception de l’instrument à sa pratique musicale.
51La conception d’instruments numériques demeure un art encore récent et de nombreuses techniques sont encore à découvrir. Max Mathews écrivait ainsi il y a 50 ans : « Il n’existe aucune limite théorique au potentiel de l’ordinateur comme source de sons musicaux ». On peut imaginer qu’il n’y a pas plus davantage de limite dans l’étendue des techniques de jeu des sons produits par ordinateur.
Bibliographie
[1] Brown Judith C., Vaughn, Kathryn C. (1996), « Pitch center of stringed instrument vibrato tones », The Journal of the Acoustical Society of America, vol. 100, no 3, p. 1728-1735.
[2] Cadoz Claude (1999), « Musique, geste, technologie », dans Les nouveaux gestes de la musique, Genevois H., de Vivo R. (dir), Marseille, Éditions Parenthèses, p. 47-92.
[3] Cance Caroline, Genevois Hugues, Dubois Danièle. (2013), « What is instrumentality in new digital musical devices? A Contribution From Cognitive Linguistics and Psychology », dans Actes du Congrès Interdisciplinaire de Musicologie 2009, et dans Castellengo M. et Genevois H. (dir), La musique et ses instruments, France, Éditions Delatour.
[4] Castellengo Michèle (1994), « La perception auditive des sons musicaux », dans Zenatti Arlette (dir), Psychologie de la musique, Paris, Presse Universitaire de France, coll. « Psychologie d’aujourd’hui », p. 56.
[5] De Cheveigné Alain (2005), « Pitch Perception Models », dans Plack Christopher J., Oxenham Andrew J., Fay Richard R., Popper Arthur N. (dir), Pitch, Birkhäuser.
[6] d’Alessandro Christophe, Castellengo Michèle (1994) « The pitch of short-duration vibrato tones », The Journal of the Acoustical Society of America, vol. 95, no 3, p. 1617-1630.
[7] d’Alessandro Christophe, Rilliard Albert, Le Beux Sylvain (2011), « Chironomic stylization of intonation », The Journal of the Acoustical Society of America, vol. 129, no 3, p. 1594-1604.
[8] d’Alessandro Christophe, Feugère Lionel, Le Beux Sylvain, Perrotin Olivier, Rilliard Albert (2014), « Drawing melodies: Evaluation of Chironomic Singing Synthesis », The Journal of the Acoustical Society of America, vol. 135, no 6, p. 3601-3612.
[9] D’Alessandro Nicolas, Dutoit Thierry (2007), « HandSketch Bi-Manual Controller, Investigation on Expressive Control Issues of an Augmented Tablet », in Proceedings of the 7th Conference on New Interfaces for Musical Expression (NIME’07).
[10] De Laubier Serge, Teruggi Daniel (1991), « The Midi Formers », in Proceedings of the ICMC, Montréal.
[11] Ferrante Isidoro (2011), « Vibrato rate and extent in soprano voice : A survey on one century of singing », The Journal of the Acoustical Society of America, vol. 130, no 3, p. 1683-1688.
[12] Feugère, Lionel, d’Alessandro Christophe (2015), « Contrôle gestuel de la synthèse vocale. Les instruments Cantor Digitalis et Digitartic », Traitement du signal, 32(4), 417-442, 2015.
[13] Flanagan James L., Saslow Michael G. (1958), « Pitch Discrimination for Synthetic Vowels », The Journal of the Acoustical Society of America, vol. 30, no 5, p. 435-442.
[14] Goudard Vincent, Genevois Hugues, Doval Boris, Ghomi Emilien (2011), « Dynamic intermediate models for audiographic synthesis », in Proceeding of the Sound and Music Conference (SMC 2011).
[15] Haury Jean (1999), « Petite histoire illustrée de l’interface clavier », in Les nouveaux gestes de la musique, Genevois Hugues et de Vivo Raphaël (dir), Éditions Parenthèses, Marseille, p. 93–110.
[16] Haury Jean (2008), « Un répertoire pour un clavier de deux touches. Théorie, notation et application musicale », in Document numérique, vol. 11, no 3-4.
[17] Kessous Loïc (2002), « Bi-manual Mapping Experimentation, with Angular Fundamental Frequency Control and Sound Color Navigation », in Proceedings of the International Conference on New Interfaces for Musical Expression (NIME’02), p. 113–114.
[18] Loriod Jeanne (1987), Technique de l’Onde électronique Martenot (vol. 1 et 2), Éditions Leduc.
[19] Park Brett, Gerhard, David (2013), « Rainboard and Musix : Building Dynamic Isomorphic Interfaces », in Proceeding of the New Musical Interface for Musical Expression (NIME’13).
[20] Perrotin Olivier, d’Alessandro Christophe (2013), « Adaptive mapping for improved pitch accuracy on touch user interfaces », in Proceedings of the 2013 International Conference on New Interfaces for Musical Expression (NIME13), Daejeon + Séoul, p. 186-189.
[21] Roads Curtis (2002), Microsound, The MIT Press.
[22] Shepard Roger N. (1964), « Circularity in Judgements of Relative Pitch », The Journal of the Acoustical Society of America, vol. 36, no 12, p. 2346-2353.
[23] Verfaille Vincent, Gustavino Catherine, Depalle Philippe (2005) « Perceptual Evaluation of Vibrato Models », in Proceedings of the Conference on Interdisciplinary Musicology (CIM05).
[24] Xenakis Iannis (1963), « Musiques formelles », Revue Musicale, no 253-254, 1963, 232 p., Réédition : Paris, Stock, 1981, 261 p.
[25] Zbyszynski Michael, Wright Matthew, Momeni Ali, Cullen Daniel (2007), « Ten Years of Tablet Musical Interfaces at CNMAT », in Proceedings of the International Conference on New Interfaces for Musical Expression, p. 100–105.
[26] Favilla Stuart, (1996), « Non-linear Controller Mapping for Gestural Control of Gamaka », in Proceedings of the International Computer Music Conference, p. 89-92.
[27] Vertegaal, Roel, Ungvary Tamas, and Kieslinger Michael (1996). « Towards a Musician’s Cockpit : Transducer, Feedback and Musical Function. » In Proceedings of the 1996 International Computer Music Conference. San Francisco, CA: International Computer Music Association, p. 308-311.
[28] Wanderley, Marcello M., Viollet Jean-Philippe, Isart Fabrice, and Rodet Xavier (2000). « On the Choice of Transducer Technologies for Specific Musical Functions. » in Proceedings of the 2000 International Computer Music Conference. San Francisco, CA: International Computer Music Association, p. 244-247.
[29] Marshall Mark T., Hartshorn Max, Wanderley Marcello M. and Levitin Daniel J. (2009) « Sensor Choice for Parameter Modulations in Digital Musical Instruments: Empirical Evidence from Pitch Modulation ». Journal of New Music Research, 38(3):241–253.
[30] Milne, A., Sethares, W.A. and Plamondon, J.,(2007) « Isomorphic Controllers and Dynamic Tuning: Invariant Fingerings Across a Tuning Continuum », Computer Music Journal, Winter, Vol. 31, no 4, p. 15-32.
[31] Dabby, Diana S. (1996). Musical variations from a chaotic mapping. Chaos: An Interdisciplinary Journal of Nonlinear Science, 6(2), 95-107.
[32] Charbonneau Gérard et Risset Jean-Claude, (1973) « Circularité de jugements de hauteur sonore »,Comptes rendus hebdomadaires des séances de l’Académie des sciences, Paris, vol. 277 B, p. 623-626.
Notes
1 Fonction de correspondance entre une variable (e.g. issue d’une interface homme-machine) et une autre variable (e.g. contrôlant la hauteur d’un son). Nous conservons ici le terme anglophone, couramment employé dans la littérature sur le sujet.
2 Patch LAM.pitch.processing.maxpat de la librairie du LAM disponible à l'adresse : https://github.com/LAM-IJLRA/lam-lib/tree/master/examples
3 Max © Cycling'74 - http://cycling74.com/
4 Équipe Lutheries - Acoustique - Musique de l'institut Jean Le Rond d'Alembert. Erreur ! Référence de lien hypertexte non valide.
5 « La hauteur par auto-corrélation » et le « pattern matching » semblent remplacer aujourd'hui les notions de « hauteur fondamentale » et « hauteur spectrale » (De Cheveigné, 2005).
6 Voir http://en.wikipedia.org/wiki/Shepard_tone pour plus de détails.
7 Citons : Ableton Push (https://www.ableton.com/en/push), Thummer (http://www.thummer.com), Dualo (http://dualo.org) et Striso (http://www.striso.org)
8 http://en.wikipedia.org/wiki/Samchillian
9 Voir quelques exemples de concerts : http://youtu.be/KAtROd5mus8
11 http://www.rogerlinndesign.com
12 https://www.roli.com/seaboard/
13 http://www.moogmusic.com/products/etherwave-theremins/theremini
14 De l'ordre de 0.1 mm sur la surface, et une fréquence d'échantillonnage de 200 Hz.
15 Tous les timbres ne se prêtent pas à cette illusion qui fonctionne essentiellement pour des sons harmoniques riches. Le « Striso » » mentionné plus haut est un instrument qui utilise cette technique.
16 http://www.huygens-fokker.org/scala/scl_format.html
17 FSR : Force Sensing Resistor - capteur de force.
18 Temps après lequel l'amplitude, de décroissance exponentielle, a été divisée par deux.
19 Également vibrato arm/bar ou tremolo arm/bar
20 Low-Frequency Oscillator
21 comme dans la synthèse par « »Glisson » de Roads (Roads, 2002)